TF2T and STFT

Moreover, Boyd and Lorberbaum (1987) showed that no deterministic (pure) strategy is evolutionarily stable in the IPD. Consider the following line of argument: a strategy S_e is robust (or "collectively stable", Boyd and Lorberbaum 1987) if for any given strategy S_i:

V(S_e|S_e)>=V(S_i|S_e) (3)

where V(S_m|S_n) is the payoff of individuals using strategy Sm when interacting with individuals using strategy S_n. Consider a randomly meeting population, consisting of n strategies with the frequencies f₁, f₂,...,f_n. Furthermore, a common strategy S_e coexists with n-1 rare strategies, so that f_e>> f_j (e unequal j). In order to fulfil this assumption, the inequality

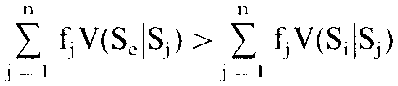(4)

needs to be satisfied. This is still the case, if for some i, V(S_e|S_e)=V(S_i|S_e). There may be even strategies S_i, for which V(S_i|S_i)=V(S_e|S_i) and (4) still is true. For example, the nice strategy TFT has the same expected fitness as another nice strategy Tit for two tats (TF2T, allowing two consecutive Ds before retaliating) when interacting, because neither ever defects. The relative fitness of TFT and TF2T is dependent upon their interaction with any third strategy. Assume this third strategy is Suspicious tit for tat (STFT, playing D in the first interaction), maintained at a low level in the population through recurrent mutation (for example). For V(TF2T|STFT)>V(TFT|STFT) TF2T can invade TFT without random drift. If (2) holds, this is always true because the more tolerant TF2T invokes cooperation in STFT, whereas the retaliatory TFT defects together with STFT. Accordingly, any deterministic strategy can be invaded and outcompeted by the joint effect of a "twin"-strategy together with another strategy. Boyd and Lorberbaum (1987) proved this general case to be true for all w>min[(T-R)/(T-P), (P-S)/(R-S)].
Lorberbaum (1994) extended the instability proof to stochastic (mixed) strategies as well. Depending on the initial set of assumptions, however, there are different types of evolutionary stability of single strategies (Bender and Swistak 1995) or of groups of strategies (see below) in the IPD. All of which have to be considered before seriously testing the model.