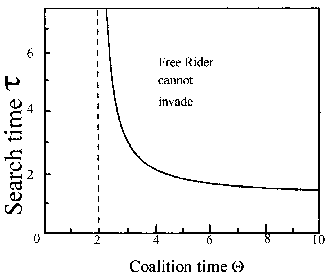
Free Rider and Rover

Soon after these findings, it became clear that a 'mobile individual using an ALLD strategy could exploit a population of cooperators, simply by switching to new partners (i.e. manipulating w for its own purposes) when the sucker ceased to cooperate (Dugatkin and Wilson 1991, Enquist and Leimar 1993). There are three components modulating the expected frequencies of cooperation: 1) If search time tau is low, individuals adopting this strategy are favoured. 2) The same is true, if the population is large enough for new, 'naive' individuals to be easily encountered. 3) The average coalition duration THETA modifies the availability of potential 'victims': a decrease in THETA will result in an increase in splitting of cooperating couples which leads to single individuals looking for new potential partners. In order to determine the extent to which these factors influence cooperation, Enquist and Leimar (1993) analysed a model in which "Free Riders" (FR), an ALLD strategy that abandons defecting partners, occur. Analogous to (3), the stability condition for TFT against a FR is V(TFT|TFT)>V(FR|TFT).

Fig. 2. For certain combinations of coalition time and search time, a population of cooperating individuals cannot be invaded by FR. The dashed line denotes the minimum average coalition time for an IPD with T=2, R=1, P=0 and S =-1. Redrawn from: Enquist, M. and Leimar, 0. 1993. The evolution of cooperation in mobile organisms. Anim. Behav. 45: 749.

In an essentially infinite population, the search time tau is assumed to be exponentially distributed (Enquist and Leimar 1993). Fig. 2 shows the relations between tau and THETA for which a cooperating population is stable against a FR. For long search times the stability condition approaches THETA>T/R. For shorter tau the coalition time has to be even longer: THETA>ThetaT(ThetaR+S) and for tau<=-S/R cooperation will never be evolutionarily stable. (Enquist and Leimar 1993; they used a different terminology. In their payoff matrix P=0 and S<0). Similar results were obtained from a slightly more intricate model by Dugatkin and Wilson (1991). Their strategy 'Rover' was exploiting cooperators in a patchy environment. As long as tau₁>tau>tau₂, they found Rover/TFT dimorphisms to be stable as well. Here tau₁ is the upper threshold above which TFT is evolutionarily stable against Rover and tau₂ the lower threshold, below which Rover sweeps to fixation (see also Feldmann and Thomas 1987 for further conditions for polymorphism stability).