Spatial chaos

As already pointed out by Axelrod and Hamilton (1981), a cluster of unconditional cooperators can invade an ALLD population. Consider a population of players distributed on the squares of a chess board. Each player interacts only with its immediate neighbours, obeying the parameters of the single-shot Prisoner's Dilemma. In the next generation, the square is inhabited by the player who scored the highest total: neighbour or previous owner. Obviously, a single cooperator perishes, but just four cooperators in a cluster can get a foothold, since each interacts with more cooperators than a defector can reach. Nowak and May (1992) used cellular automata to simulate the spatial distribution of ALLD and ALLC 'territories' in a population. Surprisingly, their analysis of this simple deterministic model, with no memories among the contestants and without any strategical refinement, revealed spatial chaos: unpredictably everchanging spatial patterns of ALLD and ALLC neither vanishing.
In addition, Fig. 5 demonstrates that for certain parameters the frequencies are converging towards asymptotic fractions f_C (and f_D=1-f_C, respectively). In spite of the stable relative frequencies, the chaotic fluctuations of the dynamic fractal last.

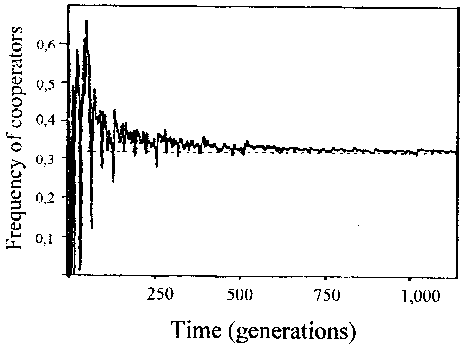
Fig. 5. The frequency of ALLC within the dynamic fractal generated by a single ALLD invading an ALLC population. (See Nowak and May 1992 for colour pictures of 'fractal kaleidoscooperation'). Redrawn from: Nowak, M. A. and May, R. M. 1992. Evolutionary games and spatial chaos. - Nature 359: 827.