Frequential chaos
If Gould and Eldredge's (1993) statement that "maintenance of stability
within species must be considered as a major evolutionary problem"
is also valid for cornpeting strategies (i.e. genotypes) in the IPD, the
findings of Nowak and Sigmund (1993b) deserve special interest. According
to their terminology, there is a set of 16 deterministic strategies S0
to S15, representing the 16 corner-points of the four-dimensional
vector space (i.e. S0 is ALLD, S9 is Pavlov, S10
is TFT, etc.). As in the last simulation, noise is taken into account by
replacing 1 by 1-e and 0 by e in the vectors; with 0 <e<<l, the
first round no longer matters (Nowak and Sigmund 1993b).
Nowak and Sigmund computed a large population consisting of S0
to S15, fi being the relative frequency of Si
in a given generation, Vi the average payoff for an Si
player and u a tiny number of invaders. Selection was computed
as described above. This yields
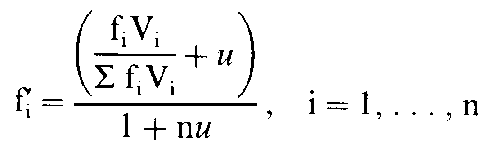 (5) (5)
where fi denotes the frequency of Si after one
generation. Eq. (5) exhibits complex dynamics. The frequencies may oscillate
periodically or display violently chaotic orbits. For example, around u
= 0.0004, S4, S6, S7 and S12
almost perish, while the other strategies oscillate vigorously. Only TFT
persists at comparatively high frequency, whereas the other oscillating
strategies come very close to fi=0. But whenever f10
(TFT) is high, it is outcompeted by a more generous strategy S11
(1, 0, 1, 1) and S9 (Pavlov), which in turn are invaded by the
parasitic S1 (0, 0, 0, I). S1 is then sacked by ALLD-like
(S0) and Grim-like (S8) rules which, as expected,
can easily be overrun by TFT (S10). However, large e favours
the domination of defective strategies and the oscillations disappear.
In this model ALLD and Grim are the only ESSs, but the introduction
of GTFT may lead to stable equilibria, where GTFT dominates (Nowak and
Sigmund 1993b).
|