|
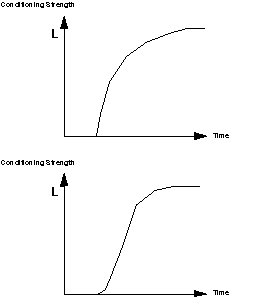
According to Rescorla and Kamin, associations are only learned when a surprising event accompanies a CS. In a normal simple conditioning experiment the US is surprising the first few times it is experienced so it is associated with salient stimuli which immediately precede it. In a blocking experiment once the association between the CS (CS1) presented in the first phase of the procedure and the US has been made the US is no longer surprising (since it is predicted by CS1). In the second phase, where both CS1 and CS2 are experienced, as the US is no longer surprising it does not induce any further learning and so no association is made between the US and CS2. This explanation was presented by Rescorla and Wagner (1972) as a formal model of conditioning which expresses the capacity a CS has to become associated with a US at any given time. This associative strength of the US to the CS is referred to by the letter V and the change in this strength which occurs on each trial of conditioning is called dV. The more a CS is associated with a US the less additional association the US can induce. This informal explanation of the role of US surprise and of CS (and US) salience in the process of conditioning can be stated as follows: dV = ab(L - V)where a is the salience of the US, b is the salience of the CS and L is the amount of processing given to a completely unpredicted US. In words: when the US is first encountered the CS has no association to it so V is zero. On the first trial the CS gains a strength of abL in its association with the US which is proportional to the saliences of the CS and the US and to the initial amount of processing given to the US. As we start trial two the associative strength is V is abL so the change in strength that occurs with the second pairing of the CS and US is ab(L - abL). It is smaller than the amount learned on the first trial and this reduction in amount that is learned reflects the fact that the CS now has some association with the US, so the US is less surprising. As more trials ensue, the equation predicts a gradually decreasing rate of learning which reaches an asymptote at L. However, the diagramm below shows: this is not what is seen when the development CS-US associations is measured over time. Instead the learning curve is sigmoidal. Rescorla has argued that the equation is consistent with observed behavior if one assumes that very small changes in associative strength are undetectable and that there is a limit to the amount of effect that very large changes can have on behavior.
There are other respects, however, where the model performs better in predicting experimental outcomes. It can also be applied to a number of CSs each of which contributes to an overall associative strength V of the US in the right hand side of the equation. It is reasonably clear that the presence of the CS salience term b in the equation lets it account for overshadowing. The meaning of the equation is clearest if the specific dVs on the left hand side are seen as referring to the increments in association between specific CSs while V on the right hand side is referring to the predictability of the US and so is the sum of all the different CS-US associations. If the conditioning strength accrued to CS1 is denoted by dV1 and that to CS2 by dV2 then our equations are dV1 = ab1(L - V)dV2 = ab2(L - V)and both dV1 and dV2 accrue to V on each trial. The amount of association directed to each CS is proportional to their salience. The equation also models blocking well. During the initial phase of a blocking experiment the associative strength of the US is increased so later, when a second CS is presented the amount of associative strength it can gain has been reduced. The critical question is, however, does the model predict experimental outcomes it was not explicitly divised for, i.e. can it be generalized? In one example the model predicts the effects of pairing two previously learned CSs on learning about a third new stimulus. If on separate occasions (not as compound stimuli) two CSs of equal salience have both been completely associated with a US then V=L for both stimuli and dV on subsequent trials is zero for both. Now a third CS in conjunction with the original pair is presented so three CSs are presented together whereas only two of them were presented singly in the past. The overall associative strength of the US is now 2L, a contribution of L from both of the original CSs. The equation predicts that there will be a negative change in associative strength on this trial proportional to the salience of the CSs: dV = ab(L - 2L)dV = -abLConducting the experiment shows: the third stimulus becomes a conditioned inhibitor of the US - it provokes a CR of the opposite quality to that produced by the other two CSs. Rescorla's explanation of the "blocking and predictability" experiment is more debatable. During phase 1 of the experiment the 'No US' are undergoing habituation. Rescorla argues that the 'No US' group learn in the first phase of the experiment that CS1 is a predictor of 'no US' and hence that, when it is followed by a US in phase 2 this US is even more surprising than it would have been normally, hence it provokes especially strong learning. His own model, however, predicts that there should be no change in the associative strength associated with the stimulus when there is no US. First, is is not very logical to assign an amount of processing devoted to a non-event if that non-event is unpredicted. Second, Rescorla's model revolves around the surprisingness of specific USs - and 'no US' must be a different US from 'US' so prior exposure to a good predictor of 'no US' should not effect the amount of processing devoted to a different US 'US'. For these, and other reasons a series of more sophisticated models have subsequently been developed in which the rate of learning is not driven by the 'surprisingness' of the US (as in the L-V term of the Rescorla-Wagner model) but by terms which represent the predictive power of individual CSs independently (for example Mackintosh's 1975 model). In this sort of model a CS which had been experienced many times unpaired with a significant US would be evaluated as having less than average predictive power. If, however, the CS had been paired with a different US during phase 1 of Rescorla's (1971) experiment, then it should be evaluated as having predictive power and hence still be associable with a different US during phase 2, reducing the 'superconditioning' to the other CS previously found. Dickinson (1976) has reported such an effect.
|